13. Countable sets, cardinality continuum PDF
Cardinality
Cardinality
Cardinality. If \(X\) and \(Y\) are nonempty sets, we define the expressions \[{\rm card\;}(X) \leq {\rm card\;}(Y) \ \ \text{ {\color{red}(injective)}},\] \[{\rm card\;}(X) = {\rm card\;}(Y)\ \ \text{ {\color{red}(bijective)}},\] \[{\rm card\;}(X) \geq {\rm card\;}(Y) \ \ \text{ {\color{red}(surjective)}},\]
to mean that there exists \(f:X \to Y\) which is injective, bijective, surjective respectively.
Cardinality - pictures 1/2
\({\rm card\;}(X) \leq {\rm card\;}(Y),\) (injective) ,.
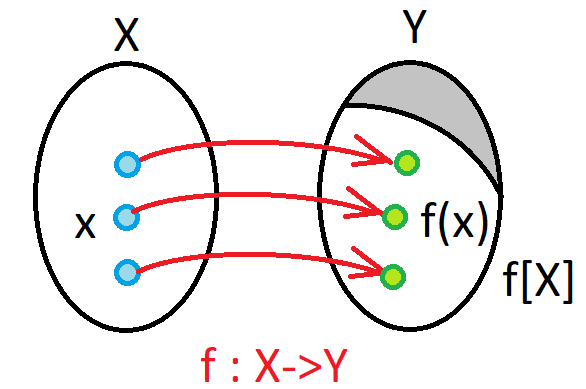
\({\rm card\;}(X) = {\rm card\;}(Y),\) (bijective).
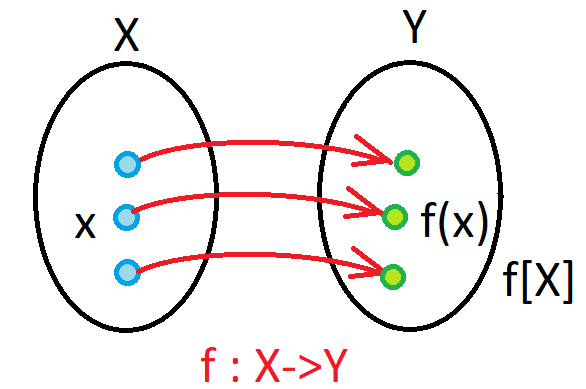
Cardinality - pictures 2/2
\({\rm card\;}(X) \geq {\rm card\;}(Y),\) (surjective).
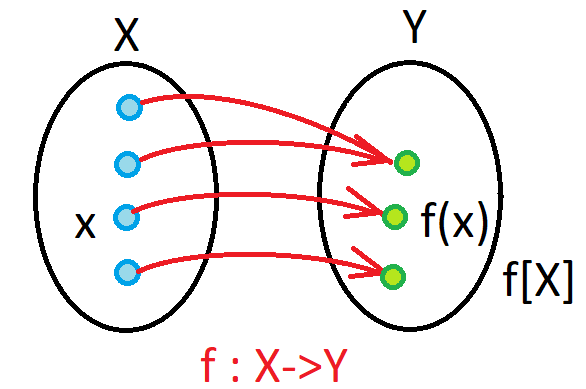
We also define \({\rm card\;}(X)<{\rm card\;}(Y)\) to mean that there is an injection but not a bijection.
We also have \({\rm card\;}(\varnothing) < {\rm card\;}(X)\) and \({\rm card\;}(X)>{\rm card\;}(\varnothing)\) for all \(X \neq \varnothing\).
\({\rm card\;}(X)\) -example
Example. Let \(X=\{1,2,3,4,\ldots\}\) and \(Y=\{101,102,103,\ldots,\}.\) Prove that \({\rm card\;}(X)={\rm card\;}(Y)\).
Solution. Let us define \(f:X \to Y\) by \(f(x)=x+100,\) then \(f\) is a bijection between \(X\) and \(Y\), so \({\rm card\;}(X)={\rm card\;}(Y)\).$$\tag*{$\blacksquare$}$$
Example. Let \(X=\{1,2,3,4,\ldots\}\) and \(Y=\{1^2,2^2,3^2,4^2,\ldots,\}.\) Prove that \({\rm card\;}(X)={\rm card\;}(Y)\).
Solution. Let us define \(f:X \to Y\) by \[f(x)=x^2,\] then \(f\) is a bijection between \(X\) and \(Y\), so \({\rm card\;}(X)={\rm card\;}(Y)\).$$\tag*{$\blacksquare$}$$
\({\rm card\;}(X)\) - example
Example. Let \(X=\{1,2,3\}\) and \(Y=\{2,4,6,8\}.\) Prove that \({\rm card\;}(X)<{\rm card\;}(Y)\).
Solution. Note that \(f(x)=2x\) is an injection from \(X\) to \(Y\), so \({\rm card\;}(X) \leq {\rm card\;}(Y)\). On the other hand, any function from \(X\) to \(Y\) takes at most \(3\) values, so it is not a surjection, so \({\rm card\;}(X)<{\rm card\;}(Y)\).$$\tag*{$\blacksquare$}$$
Example. Let \(X=[0,1]\) and \(Y=[1,3].\) Prove that \({\rm card\;}(X)={\rm card\;}(Y)\).
Solution. Let us define \(f:X \to Y\) by \[f(x)=2x+1,\] then \(f\) is a bijection between \(X\) and \(Y\), so \({\rm card\;}(X)={\rm card\;}(Y)\).$$\tag*{$\blacksquare$}$$
Proposition
Proposition. We have \[{\rm card\;}(X) \leq {\rm card\;}(Y) \iff {\rm card\;}(Y) \geq {\rm card\;}(X).\]
Proof (\(\Rightarrow\)). Assume that \({\rm card\;}(X) \leq {\rm card\;}(Y)\). This means that there is an injection \(f:X \to Y\). Thus \(f\) is a bijection \(f:X \to f[X] \subseteq Y\). Let \(f^{-1}\) be the inverse \(f^{-1}:f[X] \to X\). Pick \(x_0 \in X\) and define \(g\) by
\[g(y)=\begin{cases}f^{-1}(y) \text{ if }y \in f[X],\\ g(y)=x_0 \text{ if }y \in Y \setminus f[X]. \end{cases}\].
Then we see that \(g\) is surjective from \(Y\) to \(X\).
Proof (\(\Leftarrow\)). If \({\rm card\;}(Y) \geq {\rm card\;}(X)\), then there is a surjection \(g:Y \to X\). Then \(g[Y]=X\), and, consequently, \(g^{-1}[\{x\}]\) are nonempty and
\[g^{-1}[\{x_1\}] \cap g^{-1}[\{x_2\}] = \varnothing \quad\text{ if }\quad x_1 \neq x_2.\].
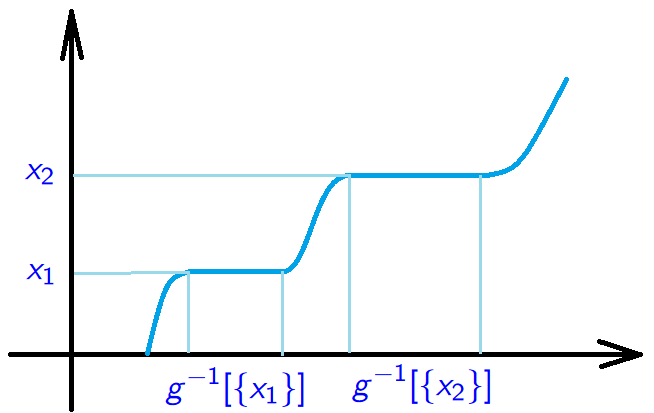
Using the axiom of choice the set \(\prod_{x \in X}g^{-1}[\{x\}] \neq \varnothing\). Taking \[f \in \prod_{x \in X}g^{-1}[\{x\}]\] we see that \(f\) is an injection from \(X\) to \(Y\). Indeed, if \(x_1 \neq x_2\), then \(f(x_1) \in g^{-1}[\{x_1\}]\) and \(f(x_2) \in g^{-1}[\{x_2\}]\), but \[g^{-1}[\{x_1\}] \cap g^{-1}[\{x_2\}] = \varnothing,\] thus \(f(x_1) \neq f(x_2)\).$$\tag*{$\blacksquare$}$$
Countable sets
\({\rm card\;}(X)\) - example
Example. Let \[X=[0,1],\] \[Y=\left\{\frac{1}{n}\;:\;n \in \mathbb{N}\right\}.\] Prove that \({\rm card\;}(X) \geq {\rm card\;}(Y)\).
Solution. One has \({\rm card\;}(Y) \leq {\rm card\;}(X)\). Indeed, define \(f:Y \to X\) by \[f(x)=x,\] which is injective, so \({\rm card\;}(X) \geq {\rm card\;}(Y)\). $$\tag*{$\blacksquare$}$$
Remark. Actually we have \({\rm card\;}(X) > {\rm card\;}(Y)\), which will be proved later.
Theorem
Theorem. For any sets \(X\) and \(Y\) \[\text{ either }\quad {\rm card\;}(X) \leq {\rm card\;}(Y)\quad \text{ or }\quad {\rm card\;}(Y) \leq {\rm card\;}(X).\]
Proof. Consider \[\mathcal{I}=\{f:\overbrace{A}^{\text{dom}} \to \overbrace{B}^{\text{rng}}: f \text{ is injection and }A \subseteq X, \ B \subseteq Y\}\] We say \(f \preccurlyeq g\) for any \(f,g \in \mathcal{I}\) if \[{\rm dom}(f) \subseteq {\rm dom}(g) \quad \text{ and } \quad f(x)=g(x)\ \text{ if } \ x \in {\rm dom}(f).\]
It is easy to see that \((\mathcal{I},\preccurlyeq)\) is a poset. Moreover, \((\mathcal{I},\preccurlyeq)\) satisfies the hypotheses of Kuratowski–Zorn’s lemma.
By Kuratowski–Zorn’s lemma, \(\mathcal{I}\) has a maximal element \(f\in \mathcal{I}\) with \({\rm dom}(f)=A\) and \({\rm rng}(f)=B\).
By maximality we deduce that \(A=X\) or \(Y=B\). If not, there are \(x_0 \in X \setminus A\) and \(y_0 \in Y \setminus B\), then \(f\) can be extended to a one-to-one map from \(A \cup \{x_0\}\) to \(B \cup \{y_0\}\). We simply set \[\widetilde{f}(x)= \begin{cases} f(x) &\text{ if } x\in A, \\ y_0 &\text{ if } x=x_0. \end{cases}\]
Then \(\widetilde{f}\) is an extension of \(f\), but this is a contradiction since \(f\) is a maximal element in \(\mathcal{I}\). Hence either \[A=X, \quad \text{ then } \quad {\rm card\;}(X) \leq {\rm card\;}(Y),\] or \[B=Y, \quad \text{ then } \quad {\rm card\;}(Y) \leq {\rm card\;}(X),\] and the proof is finished. $$\tag*{$\blacksquare$}$$
Banach lemma
Banach lemma. Let \(f:A \to B\) and \(g:B \to A\) be injections. Then there are sets \(A_1,A_2,B_1,B_2\) such that
\(A_1 \cup A_2=A\) and \(A_1 \cap A_2 = \varnothing\),
\(B_1 \cup B_2=B\) and \(B_1 \cap B_2 = \varnothing\),
\(f[A_1]=B_1\) and \(f[A_2]=B_2\).
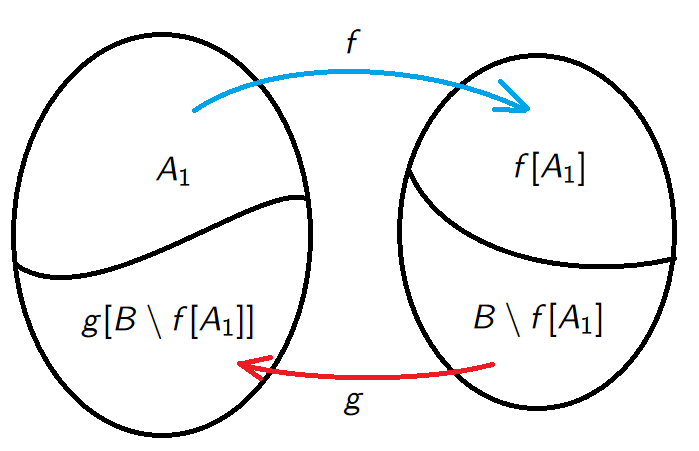
Proof. Consider the map \(\Phi:P(A) \to P(A)\) defined by \[\Phi(X)=A \setminus g[B \setminus f[X]] \quad \text{ for } \quad X \in P(X).\]
Since \(g\) is injective we note that \[\Phi\left[\bigcup_{t \in I}A_t\right]=\bigcup_{t \in I}\Phi[A_t]\] for any family \((A_t)_{t \in I}\) such that \(A_t \subseteq A\) for all \(t\in I\). Consider \[\Omega=\varnothing \cup \Phi[\varnothing] \cup \Phi \circ \Phi[\varnothing] \cup \ldots \cup \overbrace{\Phi \circ \Phi \circ \ldots \circ \Phi}^n[\varnothing] \cup \ldots,\] in other words \[\Omega=\bigcup_{n=0}^\infty \Phi^n[\varnothing].\]
Then \[\begin{aligned} \Phi[\Omega]=\bigcup_{n=0}^{\infty}\Phi^{n +1}[\varnothing] =\bigcup_{n=1}^{\infty}\Phi^{n}[\varnothing] =\left(\bigcup_{n=1}^{\infty}\Phi^{n}[\varnothing]\right) \cup \varnothing =\bigcup_{n=0}^{\infty}\Phi^{n}[\varnothing] =\Omega, \end{aligned}\] thus the set \(\Omega\) if a fixed point of \(\Phi\), i.e. \(\Phi[\Omega]=\Omega\). Taking \[A_1=\Omega, \ \ A_2=A \setminus A_1,\] \[B_1=f[A_1], \ \ B_2=B \setminus B_1\] we obtain
\[\begin{aligned} A_1=\Phi[A_1]=A \setminus g[B \setminus f[A_1]]=A \setminus g[B \setminus B_1]=A \setminus g[B_2], \end{aligned}\] thus \[\begin{aligned} A_2=A \setminus A_1=A \setminus (A \setminus g[B_2])=g[B_2]. \end{aligned}\]
Cantor–Bernstein–Schröder theorem
Cantor–Bernstein–Schröder theorem. If \({\rm card\;}(X) \leq {\rm card\;}(Y)\) and \({\rm card\;}(Y) \leq {\rm card\;}(X)\), then \({\rm card\;}(X)={\rm card\;}(Y)\).
Proof. By Banach lemma there are \(A_1,A_2,B_1,B_2\) such that \[A_1 \cup A_2=X, \ \ f[A_1]=B_1, \ \ A_1 \cap A_2 =\varnothing\] \[B_1 \cup B_2=X, \ \ g[B_2]=A_2, \ \ B_1 \cap B_2 =\varnothing\] whenever \(f:X \to Y\) and \(g:Y \to X\) are injections. Define \(h:X \to Y\) by setting
\[h(x)=\begin{cases} f(x) &\text{ if }x \in A_1,\\ g^{-1}(x) &\text{ if }x \in A_2. \end{cases}\].
Then we see that \(h\) is a bijection between \(X\) and \(Y\).$$\tag*{$\blacksquare$}$$
Cantor–Bernstein–Schröder theorem - example
Example. Let \(X=[0,1], \ \ Y=(0,1).\) Prove that \({\rm card\;}(X) = {\rm card\;}(Y)\).
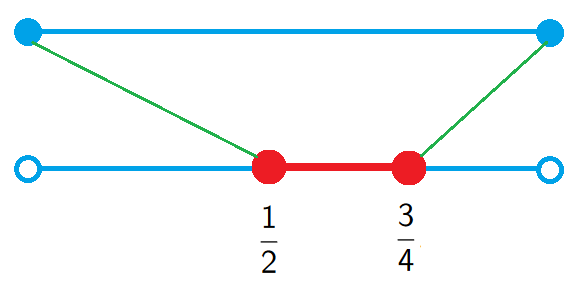
Solution. Note that \({\rm card\;}(Y) \leq {\rm card\;}(X)\), because \(f(x)=x\) is injective. Then, let us prove that \({\rm card\;}(X) \leq {\rm card\;}(Y)\). We define \[g(x)=\frac{x}{4}+\frac{1}{2}.\] One can check that \(g\) is injective, so, by Cantor–Bernstein–Schröder theorem, \({\rm card\;}(X)={\rm card\;}(Y)\).$$\tag*{$\blacksquare$}$$
Cantor’s theorem
Cantor’s Theorem. For any set \(X\) we have \({\rm card\;}(X) < {\rm card\;}(P(X))\).
Proof. The map \(f:X \to P(X)\) defined by \(f(x)=\{x\}\) is an injection from \(X\) to \(P(X)\). Thus \({\rm card\;}(X) \leq {\rm card\;}(P(X))\).
We now show that there is no bijection between \(X\) and \(P(X)\). Let \(g:X \to P(X)\) and consider the set \[{\color{red}Y=\{x \in X\;:\; x \not\in g(x)\}} \in P(X).\] Then we claim that \(Y \not\in g[X]\).
If \[Y=\{x \in X\;:\; x \not\in g(x)\} \in g[X],\] then there is \(x_0 \in X\) so that \({\color{blue}g(x_0)=Y}\).
On the one hand \[x_0 \in Y \iff {\color{red} x_0 \not\in g(x_0).}\]
On the other hand \[x_0 \in Y \iff {\color{blue}x_0 \in g(x_0)}.\]
Thus \[x_0 \in g(x_0) \iff x_0 \not\in g(x_0),\] which is impossible, and we conclude \({\rm card\;}(X)<{\rm card\;}(P(X))\).$$\tag*{$\blacksquare$}$$
Countable set
Countable set. A set \(X\) is called countable (or denumerable) if \[{\rm card\;}(X) \leq {\rm card\;}(\mathbb{N}).\]
Example 1. In particular, finite sets are countable and for these sets it is convenient to interpret \({\rm card\;}(X)\) as the number of elements in \(X\):
\[{\rm card\;}(X)=n \iff {\rm card\;}(X)={\rm card\;}(\{1,2,\ldots,n\}).\]
Example 2. If \(X\) is countable but not finite, we say that \(X\) is countably infinite.
Countable sets - example
The set \(\mathbb{N} \times \mathbb{N}\) is countable, i.e. \({\rm card\;}(\mathbb{N} \times \mathbb{N})={\rm card\;}(\mathbb{N})\). Note that

can be listed as a sequence \[(1,1),{\color{red}(1,2),(2,1)},{\color{blue}(1,3),(2,2),(3,1)},{\color{brown}(1,4),(2,3),(3,2),(4,1)},{\color{purple}(5,1),(4,2)},\ldots\] establishing a bijection between \(\mathbb{N} \times \mathbb{N}\) and \(\mathbb{N}\).
Proposition
Proposition.
If \(X\) and \(Y\) are countable, so is \(X \times Y\).
If \(A\) is countable and \(X_{\alpha}\) is countable for all \(\alpha \in A\), then \[\bigcup_{\alpha \in A}X_{\alpha} \text{ is countable.}\]
If \(X\) is countably infinite then \({\rm card\;}(X)={\rm card\;}(\mathbb{N})\).
Proof of (a). To prove (a) it suffices to show that \({\rm card\;}(\mathbb{N} \times \mathbb{N})={\rm card\;}(\mathbb{N})\), but it was shown in the previous example.
Proof of (b). For each \(\alpha \in A\) there is a surjection \(f_{\alpha}:\mathbb{N\to X_{\alpha}}\) (here we have used the axiom of choice).
Then the map \(f:\mathbb{N} \times \mathbb{N} \to \bigcup_{\alpha \in A}X_{\alpha}\) defined by
\[f(n,\alpha)=f_{\alpha}(n)\] is surjective and we are done. Alternatively, to prove \[{\rm card\;}\left(\bigcup_{\alpha \in A}X_{\alpha}\right) \leq {\rm card\;}(\mathbb{N}),\] we can also proceed as follows \[X_1=\{x_{1,1},x_{1,2},x_{1,3},x_{1,4},\ldots\}\] \[{\color{red}X_2=\{x_{2,1},x_{2,2},x_{2,3},x_{2,4},\ldots\}}\] \[{\color{blue}X_3=\{x_{3,1},x_{3,2},x_{3,3},x_{3,4},\ldots\}}\] \[\cdots\] \[\bigcup_{j \in \mathbb{N}}X_j=\{x_{1,1},{\color{red}x_{1,2}},{\color{red}x_{2,1}},{\color{blue}x_{1,3}},{\color{blue}x_{2,2}},{\color{blue}x_{3,1}},\ldots\}.\]
Proof of (c).
We can assume that \(X\) is an infinite
subset of \(\mathbb{N}\).
Let \(f(1)\) be the smallest element of
\(X\) and define inductively \[f(n)=\min\big\{X \setminus
\{f(1),f(2),\ldots,f(n-1)\}\big\}.\]
Then it can be easily verified that \(f\) is a bijection from \(\mathbb{N}\) to \(X\).$$\tag*{$\blacksquare$}$$
Corollary. \(\mathbb{Z}\) and \(\mathbb{Q}\) are countable.
Proof. One has \(\mathbb{Z}=\mathbb{N} \cup \{0\} \cup \{-n\;:\; n \in \mathbb{N}\}\) and \[\mathbb{Q}=\bigcup_{n \in \mathbb{N}}\{\frac{m}{n}\;:\;m \in \mathbb{Z}\}.\]
Note also that \[\qquad {\rm card\;}(\mathbb{Q})={\rm card\;}(\mathbb{N})={\rm card\;}(\mathbb{N} \cup \{0\})={\rm card\;}(\mathbb{Z}). \qquad \tag*{$\blacksquare$}\]
Countable sets - example
Example. Prove that the following set is countable \(X=\{(n,m,k)\;:\; n,m,k \in \mathbb{N}\}.\)
Solution. Fix \(k \in \mathbb{N}\). It is clear that \(f(n,m)=(n,m,k)\) is a bijection between \(\mathbb{N} \times \mathbb{N}\) and \(A_k=\{(n,m,k)\;:\; n,m \in \mathbb{N}\}\), so \(A_k\) is countable. Then we write \(X=\bigcup_{k \in \mathbb{N}}A_k\) and use the previous theorem.$$\tag*{$\blacksquare$}$$
Example. Prove that the set \(\mathbb{Q} \times \mathbb{Q}\) is countable.
Solution. Fix \(q \in \mathbb{Q}\). It is easy to check that \(f(x)=(x,q)\) is bijection between \(\mathbb{Q}\) and \(A_q=\{(r,q)\;:\; r \in \mathbb{Q}\}\). Hence \(A_q\) is countable. We write \[\mathbb{Q} \times \mathbb{Q}=\bigcup_{q \in \mathbb{Q}}A_q\] and use the previous theorem.$$\tag*{$\blacksquare$}$$
Proposition
Proposition. \(\{0,1\}^{\mathbb{N}_0}\) is uncountable.
Proof. Suppose that the set \(\{0,1\}^{\mathbb{N}_0}\) is countable, then \[\{0,1\}^{\mathbb{N}_0}=\{\alpha_0,\alpha_1,\alpha_2,\ldots\}.\]
\[\alpha_0: \ \ \ {\color{red}\alpha_0(0)}, \alpha_0(1), \alpha_0(2),\ldots\] \[\alpha_1: \ \ \ \alpha_1(0), {\color{red}\alpha_1(1)}, \alpha_1(2),\ldots\] \[\alpha_2: \ \ \ \alpha_2(0), \alpha_2(1), {\color{red}\alpha_2(2)},\ldots\] \[\ldots\]
consider a new sequence \(\Delta:\mathbb{N}_0 \to \{0,1\}\) defined by \(\Delta(n)=1-\alpha_n(n).\) Then \(\Delta \neq \alpha_n\) for all \(n \in \mathbb{N}_0\), thus \(\Delta \not\in \{\alpha_n\;:\;n \in \mathbb{N}_0\}\), but \(\Delta \in \{0,1\}^{\mathbb{N}_0},\) contradiction.$$\tag*{$\blacksquare$}$$
Cardinality continuum
Cardinality continuum
Cardinality continuum. A set \(X\) is said to have cardinality continuum if \[{\rm card\;}(X)={\rm card\;}(\mathbb{R}).\]
We shall write \({\rm card\;}(X)=\mathfrak{c}\) iff \({\rm card\;}(X)={\rm card\;}(\mathbb{R}).\)
Theorem. \[{\rm card\;}(P(\mathbb{N}))={\rm card\;}(\{0,1\}^{\mathbb{N}})={\rm card\;}(\mathbb{R}).\]
We first show that \[{\rm card\;}(P(\mathbb{N}))={\rm card\;}(\{0,1\}^{\mathbb{N}}).\]
Define \(F:P(\mathbb{N}) \to \{0,1\}^{\mathbb{N}}\) by setting
\[F(A)=\chi_{A} \in \{0,1\}^{\mathbb{N}},\]. \[\chi_{A}(x)=\begin{cases} 1 \text{ if }x \in A,\\ 0 \text{ if }x\not\in A. \end{cases}\]
Example. If \(A=\{1,2,3,5,7,9\}\), then \(\chi_A\) can be identified with the sequence \[(\underbrace{1}_{{\color{red}1}},\underbrace{1}_{{\color{red}2}},\underbrace{1}_{{\color{red}3}},\underbrace{0}_{{\color{red}4}}, \underbrace{1}_{{\color{red}5}}, \underbrace{0}_{{\color{red}6}}, \underbrace{1}_{{\color{red}7}}, \underbrace{0}_{{\color{red}8}}, \underbrace{1}_{{\color{red}9}}, \underbrace{0}_{{\color{red}10}},\underbrace{0}_{{\color{red}11}},\ldots)\]
Our aim is to show that \(F\) is a bijection.
Let \(A,B \subseteq \mathbb{N}\) be such that \(A \neq B\), then we show that \(F(A) \neq F(B)\). Since \(A \neq B\) (wlog) there exists \(x_0 \in A \setminus B\), thus \[1=\chi_{A}(x_0) \neq \chi_{B}(x_0)=0 \quad \iff \quad F(A) \neq F(B),\] which proves that \(F:P(\mathbb{N}) \to \{0,1\}^{\mathbb{N}}\) is injective.
To show that \(F\) is surjective take \(\alpha=(\alpha_n)_{n \in \mathbb{N}} \in \{0,1\}^{\mathbb{N}}\) and consider \[E=\{n \in \mathbb{N}\;:\;\alpha_n=1\}.\] then \[F(E)=\chi_E=\alpha \quad \iff \quad 1=\alpha_n=\chi_E(n)=1.\]
It remains to prove that \[{\rm card\;}(P(\mathbb{N}))={\rm card\;}(\mathbb{R}).\]
We first show that \({\rm card\;}(P(\mathbb{N})) \leq {\rm card\;}(\mathbb{R})\).
We now construct an injection \(f:P(\mathbb{N}_0) \to \mathbb{R}\) by setting \[f(A)=\sum_{n \in A}\frac{2}{3^{n+1}}\quad \text{ for any } \quad A \subseteq \mathbb{N}_0.\]
\(f(\mathbb N_0)=1\), since \[\sum_{n =0}^N\frac{2}{3^{n+1}}=\frac{2}{3}\frac{1-\frac{1}{3^{N+1}}}{1-\frac{1}{3}}=1-\frac{1}{3^{N+1}} \leq 1.\]
Now we show that \(f:P(\mathbb{N}_0) \to \mathbb{R}\) is injective. Let \(A,B \subseteq \mathbb{N}\) be such that \(A \neq B\). Let \[n_0=\min\{n \in \mathbb{N}_0\colon \chi_A(n)\neq \chi_B(n)\}.\] Wlog we can assume \(n_0 \in B \setminus A\). Then \[\begin{aligned} f(A)&=\sum_{n \in A}\frac{2}{3^{n+1}}={\color{blue}\sum_{\substack{n \in A \\ n<n_0}}\frac{2}{3^{n+1}}} +\sum_{\substack{n \in A \\ n>n_0}}\frac{2}{3^{n+1}} \\ &\le {\color{blue}\sum_{\substack{n \in B\\ n<n_0}}\frac{2}{3^{n+1}}}+\sum_{n \in (n_0,\infty)}\frac{2}{3^{n+1}} \\ &< {\color{blue}\sum_{\substack{n \in B\\ n<n_0}}\frac{2}{3^{n+1}}}+\frac{2}{3^{n_0+1}} \leq f(B). \end{aligned}\]
We have used \(f((n_0,\infty) \cap \mathbb{N}_0)=\frac{1}{3^{n_0+1}}<\frac{2}{3^{n_0+1}}\) (check this!).
Hence \(f(A) \neq f(B)\) as desired, yielding \({\rm card\;}(P(\mathbb{N}_0)) \leq {\rm card\;}(\mathbb{R})\).
Since \({\rm card\;}(\mathbb{N}_0)={\rm card\;}(\mathbb{Q})\) thus \({\rm card\;}(P(\mathbb{N}_0))={\rm card\;}(P(\mathbb{Q}))\). Now define \(g:\mathbb{R} \to P(\mathbb{Q})\) by \[g(x)=\{r \in \mathbb{Q}\colon r<x\} \quad \text{ for any } \quad x\in \mathbb{R}.\]
It is easy to see that \(g\) is injective, thus \[{\rm card\;}(\mathbb{R}) \leq {\rm card\;}(P(\mathbb{Q}))={\rm card\;}(P(\mathbb{N}_0)).\]
By the Cantor–Bernstein–Schröder theorem \[{\rm card\;}(\mathbb{R})={\rm card\;}(P(\mathbb{N}_0))={\rm card\;}(\{0,1\}^{\mathbb{N}}).\tag*{$\blacksquare$}\]
Remarks
If \({\rm card\;}(X) \geq \mathfrak{c}\), then \(X\) is uncountable.
\({\rm card\;}(\mathbb{R} \times \mathbb{R})={\rm card\;}(\mathbb{R})\).
\({\rm card\;}(\{0,1\}^{\mathbb{N}_0} \times \{0,1\}^{\mathbb{N}_0})={\rm card\;}(\{0,1\}^{\mathbb{N}_0})\).
\({\rm card\;}(\mathbb{R}^k)={\rm card\;}(\mathbb{R})\) for any \(k\in \mathbb N\).
If \({\rm card\;}(X) \leq \mathfrak{c}\) and \({\rm card\;}(Y) \leq \mathfrak{c}\), then \({\rm card\;}(X \times Y) \leq \mathfrak{c}\).
If \({\rm card\;}(A) \leq \mathfrak{c}\) and \({\rm card\;}(X_{\alpha}) \leq \mathfrak{c}\) for any \(\alpha \in A\), then \[{\rm card\;}\left(\bigcup_{\alpha \in A}X_{\alpha}\right) \leq \mathfrak{c}.\]
Uncountable sets - example
Example. Prove that \({\rm card\;}(\mathbb{R})={\rm card\;}([0,1])\).
Solution. Define \(f:\mathbb{R} \to [0,1]\) by \(f(x)=\frac{x}{|x|+1}.\) One can verify that \(f\) is a bijection between \(\mathbb{R}\) and \([0,1]\).$$\tag*{$\blacksquare$}$$
Example. Determine \({\rm card\;}(X)\), where \(X\) is \[\{[n,n+1)\;:\;n \in \mathbb{N}\}.\]
Solution. We will prove that \({\rm card\;}(X)={\rm card\;}(\mathbb{N})\). Define \[f([n,n+1))=n.\] It is easy to verify that \(f\) is bijection between \(\mathbb{N}\) and \(X\).$$\tag*{$\blacksquare$}$$
Example. Determine \({\rm card\;}(X)\), where \(X\) is any infinite set of pairwise disjoint closed intervals.
Solution. We will prove that \(X\) is countably infinite. Let us define the function \(f:X \to \mathbb{Q}\) by setting \[f(I)=q,\] where \(q\) is any rational number contained in interval \(I \in X\). Then \(f\) is injective, so \({\rm card\;}(X) \leq {\rm card\;}(\mathbb{N})\). $$\tag*{$\blacksquare$}$$