Well ordered sets

Well ordering principle and induction principle

\[\forall_{A \subseteq \mathbb{N}_0}\left(0 \in A \text{ and }\forall_{k \in \mathbb{N}}(k \in A \Longrightarrow (k+1) \in A) \text{ then }A=\mathbb{N}_0\right)\]

The maximum principle

\[\exists_{M \in \mathbb{N}_0} \ \ \forall_{a \in A} \ \ a \leq M\]

Induction principle: classical example

Solution. Let \(A\) be the set of \(n\) for which [eq:n] holds. \[A=\left\{n \in \mathbb{N}_0: \sum_{k=0}^{n}k=\frac{n(n+1)}{2}\right\}.\] Our goal is to show that \(A = \mathbb{N}_0\). We will use the induction principle. We have to check the base step and the induction step.

Solution

• We verify (base step): \(0 \in A\). Indeed, one has \[\sum_{k=0}^0 k = 0 =\frac{0(0+1)}{2},\quad \text{ thus }\quad 0 \in A.\]

• We verify (induction step): \(n \in A \Longrightarrow n+1 \in A\). If \(n \in A\), then \[{\color{blue} \sum_{k=0}^{n}k=\frac{n(n+1)}{2}.}\] Our goal is to prove that \(n+1 \in A\). We calculate \[\sum_{k=0}^{n+1}k={\color{blue}\sum_{k=0}^{n}k}+(n+1) ={\color{blue}\frac{n(n+1)}{2}}+(n+1)=\frac{(n+1)(n+2)}{2}.\]

Three principles

Our goal

Our goal is to prove that the statements (A), (B), and (C) are equivalent.

In order to prove that, we will show:

1. (A) \(\Rightarrow\) (B)

2. (B) \(\Rightarrow\) (A)

3. (A) \(\Rightarrow\) (C)

4. (C) \(\Rightarrow\) (A)

(A) \(\Rightarrow\) (B)

• If \(A\) is a set of non-negative integers such that

  1. \(0 \in A\).

  2. Whenever \(A\) contains a number \(n\), it also contains \(n+1\).

• We want to establish \(A=\mathbb{N}_0\).

• Suppose for contradiction that \(A \neq \mathbb{N}_0\). Then \(\mathbb{N}_0 \setminus A \neq \varnothing\). By well ordering principle (A) there is the smallest element \(m\) of \(\mathbb{N}_0 \setminus A\).

  1. Since \(0 \in A\), we have \(m \neq 0\),

  2. Observe that \(m-1 \in A\), because otherwise \(m-1 \in \mathbb{N}_0 \setminus A\), which contradicts the fact that \(m\) is the smallest element of \(\mathbb{N}_0 \setminus A\). But if \(m-1\in A\), then by (2) we have \(m \in A\), which is impossible.

• The implication (A) \(\Rightarrow\) (B) follows. $$\tag*{$\blacksquare$}$$

(B) \(\Rightarrow\) (A)

Let \(A \subseteq \mathbb{N}_0=\{0,1,2,\ldots\}\) such that \(A \neq \varnothing\). Suppose for contradiction that \(A\) does not have a least element.

• It is easy to see that \(0 \not\in A\), because otherwise it would be a minimal element of \(A\) (as \(0\) is the minimal element of \(\mathbb{N}_0\)).

• We also see \(1 \not \in A\), otherwise it is a minimal element of \(A\).

• We continue and assume that \(1,2,\ldots,n \not \in A\). Then \(n+1 \not\in A\), otherwise \(n+1\) is the smallest element of \(A\).

Now use the principle of induction and conclude that \(A =\varnothing\).$$\tag*{$\blacksquare$}$$

(A) \(\Rightarrow\) (C)

• Suppose that \(A \neq \varnothing\) and bounded. \[\underbrace{\exists}_{\text{there exists}} M \in \mathbb{N}_0 \ \ \underbrace{\forall}_{\text{for all}} a \in A \ \ a \leq M\]

• This means that \(M-a \geq 0\) for all \(a \in A\). Let us consider the set \[B=\{M-a\;:\; a \in A\} \neq \varnothing.\]

• By the well ordering principle (A) there is \(b \in A\) such that \(M-b\) is the smallest element of \(B\).

• Thus \[M-b \leq M-a\] for all \(a \in A\), equivalently \(a \leq b\) for all \(a \in A\).$$\tag*{$\blacksquare$}$$

(C) \(\Rightarrow\) (A)

• Let \(A \subseteq \mathbb{N}_0\), \(A \neq \varnothing\). We show that \(A\) has a minimal element. Let \[B=\{n \in \mathbb{N}_0\;:\; n \leq a \text{ for every }a\in A\}=\{n \in \mathbb{N}_0\;:\; \forall a \in A\ n \leq a \}\]

• The set \(B\) is bounded and \(0 \in B\) since \(0 \leq n\) for any \(n \in \mathbb{N}_0\). Thus, by the maximum principle (C) we are able to find \(b_0 \in B\) such that \(b_0\) is maximal in \(B\). We see \[\forall a \in A \ \ \forall b \in B \ \ b \leq b_0 \leq a.\]

• The proof will be completed if we show \(b_0 \in A\).

• Assume for contradiction \(b_0 \neq a\) and \(b_0 \leq a\) for all \(a \in A\). Thus \(b_0<a\) for all \(a \in A\). Hence \[b_0+1 \leq a\] for any \(a \in A\). Then \(b_0+1 \in B\), but \(b_0\) is the maximal element of \(B\), which gives contradiction.$$\tag*{$\blacksquare$}$$

Induction: example

Solution. Let \(A\) be the set of \(n\) for which \(6\) divides \(7^n-1\). \[A=\left\{n \in \mathbb{N}_0\;:\; 6 \text{ divides }7^n-1\right\}\]

Our goal is to show \(A = \mathbb{N}_0\). We will use the induction principle.

Base step. We have \(7^0-1=0\) hence \(6\) divides \(0\). Thus \(0 \in A\).

Induction step. We now verity that \(n \in A \Longrightarrow n+1 \in A\). Indeed, \[\begin{aligned} 7^{n+1}-1&=7^{n+1}-{\color{red}7^n}+{\color{red}7^n}-1 \\&=(7-1)7^n+7^n-1 \\=&\underbrace{6 \cdot 7^n}_{\text{divisible by }6}+\underbrace{7^n-1}_{\text{divisible by }6 \text{ since }n \in A} \end{aligned}\] $$\tag*{$\blacksquare$}$$

Well ordering principle: example

Solution. In the proof, we will use the well ordering principle. Let \(A\) be the set of integers \(n\in \mathbb N_0\) such that \(a_n\neq2 \cdot 3^n-3 \cdot 2^n\). We will show that \(A=\varnothing\). Suppose for a contradiction that \(A\neq\varnothing\) and let \(n_0\) be the smallest element of this set. Since \[a_0=2 \cdot 1 -3 \cdot 1=-1,\] \[a_1=2\cdot 3^1-3\cdot 2^1=0\] we have \(n_0 \neq 0,1\). By the minimality of \(n_0\) we have \[a_n=2 \cdot 3^n-3 \cdot 2^n\] for all \(0\le n<n_0\).

Solution

Using the reccurence definition \[a_{n_0}=5a_{n_0-1}-6a_{n_0-2}\] we obtain \[\begin{aligned} 2 \cdot 3^{n_0}-3 \cdot 2^{n_0}\neq a_{n_0}&=5a_{n_0-1}-6a_{n_0-2}\\ &=5 \cdot(2 \cdot 3^{n_0-1}-3 \cdot 2^{n_0-1})-6\cdot(2 \cdot 3^{n_0-2}-3 \cdot 2^{n_0-2})\\&=2 \cdot 3^{n_0}-3 \cdot 2^{n_0}, \end{aligned}\] which contradicts the minimality of \(n_0\). This shows that \(A=\varnothing\). $$\tag*{$\blacksquare$}$$

The equation \(p^2=2\) has no solution in rational numbers

The rational numbers are \[\mathbb{Q}=\left\{\frac{n}{m}\;:\; n \in \mathbb{Z},\; m \in \mathbb{Z} \setminus \{0\} \right\}.\]

• The numbers \(6\) and \(42\) are not relatively prime.

• The numbers \(21\) and \(10\) are relatively prime.

• The number \(n \in \mathbb{N}_0\) is even if it is divisable by \(2\).

• The number \(n \in \mathbb{N}\) is odd if it is not divisable by \(2\).

The solution of \(p^2=2\)

The solution of \(p^2=2\) exists as a geometric length of the diagonal of the square of side-length 1.

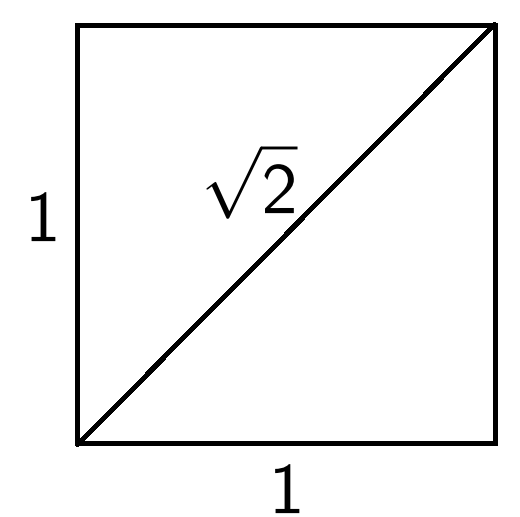
Sets without minimal and maximal elements

Let \[A=\{p \in \mathbb{Q}\;:\;p>0,\; p^2<2\},\] \[B=\{p \in \mathbb{Q}\;:\;p>0,\; p^2>2\},\]

We will show that:

• \(A\) contains no largest number,

• \(B\) contains no smallest number.

It is also easy to see that \[\mathbb Q_+=\{x\in \mathbb Q: x>0\}=A\cup B.\]

Set \(A\)

• For \(p \in A\) we define \[\label{eq:pq_1} q=p-\frac{p^2-2}{p+2}=\frac{2p+2}{p+2}.\]

• Then we have \[\label{eq:pq_2} q^2-2=\frac{2(p^2-2)}{(p+2)^2}.\]

• Since \(p^2-2<0\), it follows by [eq:pq_1] that \(p<q\).

• Then, [eq:pq_2] shows that \(q^2<2\), so \(q \in A\).

Set \(B\)

• Again, for \(p \in B\) we define \[\label{eq:pq_3} q=p-\frac{p^2-2}{p+2}=\frac{2p+2}{p+2}.\]

• Then we have \[\label{eq:pq_4} q^2-2=\frac{2(p^2-2)}{(p+2)^2}\]

• This time \(p^2-2>0\), it follows by [eq:pq_3] that \(q<p\).

• Then, [eq:pq_4] shows that \(q^2>2\), so \(q \in B\).

Concepts of largeness and smallness

• The second property follows from the first one by taking \(x=\frac{1}{y}\). Thus it suffices to prove the first statement.

• If \(x\in \mathbb{Q}\) and \(x\le 0\), then there is nothing to do. Suppose that \(x>0\), then \(x=\frac{p}{q}\) for some \(p, q\in \mathbb{N}\). Consider the set \[A=\{n\in\mathbb{N}_0: n\le x\}.\]

• This set is nonempty since \(x>0\). We see that \(m\in A\) iff \(p-qm\ge0\). Consider now the set \[B=\{p-qn: n\in A\}\subset \mathbb N_0, \qquad \text{ and } \qquad B\neq \varnothing.\]

• By the well-ordering principle \(B\) contains the smallest element, say \(p-qm_0\) for some \(m_0\in A\). Thus for all \(n\in A\) we have \[p-qm_0\le p-qn \quad \Longleftrightarrow \quad n\le m_0\le x.\]

• Now we see that \(x< m_0+1\) has desired property.$$\tag*{$\blacksquare$}$$