22. Exponential Function and Natural Logarithm Function; Power Series and Taylor's theorem PDF
The exponential function
The exponential function
The exponential function. We define \[E(z)=\sum_{n=0}^{\infty}\frac{z^n}{n!}, \quad \text{ for } \quad z \in \mathbb{R}.\]
Observe that \(|E(z)| \leq \sum_{n=0}^{\infty}\frac{|z|^n}{n!}<\infty.\) Thus the ratio test shows that the series converges absolutely for any \(z \in \mathbb{R}\).
Recall. If \(\sum_{n=0}^{\infty}a_n\) converges absolutely, \({\color{red}\sum_{n=0}^{\infty}a_n=A}\), and \({\color{blue}\sum_{n=0}^{\infty}b_n=B}\), and \[c_n=\sum_{k=0}^n a_kb_{n-k}, \quad \text{ for } \quad n=0,1,2,\ldots .\] Then \(\sum_{k=0}^\infty c_k={\color{red}A}{\color{blue}B}\).
Properties of the exponential function 1/4
Applying this result to absolutely convergent series \(E(z)\), \(E(w)\) we obtain
(*). \[E(z)E(w)=E(z+w) \quad \text{ for } \quad z,w \in \mathbb{R}.\]
Proof of (*). Indeed, \[\begin{aligned} E(z)E(w)&=\left(\sum_{n=0}^{\infty}\frac{z^n}{n!}\right)\left(\sum_{m=0}^{\infty}\frac{w^m}{m!}\right) \underbrace{=}_{{\color{red}Recall}}\sum_{n=0}^{\infty}\sum_{k=0}^{n}\frac{z^kw^{n-k}}{k!(n-k)!} \\&=\sum_{n=0}^{\infty}\frac{1}{n!}\sum_{k=0}^n {n \choose k}z^kw^{n-k}=\sum_{n=0}^{\infty}\frac{(z+w)^n}{n!}=E(z+w). \end{aligned}\] In the last line we have used the Binomial theorem. $$\tag*{$\blacksquare$}$$
Properties of the exponential function 2/4
As the consequence we obtain
(**). \[E(z)E(-z)=E(z-z)=E(0)=1.\]
This shows that \(E(z) \neq 0\) for all \(z \in \mathbb{R}\).
We have \(E(x)>0\) if \(x>0\), giving \(E(x)>0\) for all \(x \in \mathbb{R}\) by (**).
It is easy to see that \[\lim_{x \to \infty}E(x)=+\infty\quad \text{ since } \quad E(x)=\sum_{n=0}^{\infty}\frac{x^n}{n!}.\]
Consequently by (**) we obtain \[\lim_{x \to \infty}E(-x)=0\quad \text{ since } \quad E(-x)=\frac{1}{E(x)}.\]
Properties of the exponential function 3/4
If \(0<x<y\) then \[E(x)=\sum_{n=0}^{\infty}\frac{x^n}{n!}<\sum_{n=0}^{\infty}\frac{y^n}{n!}=E(y).\]
Since \(E(x)E(-x)=1\) thus \[E(-y)<E(-x),\] hence \(E\) is strictly increasing on \(\mathbb{R}\).
If \(x \in \mathbb{R}\) then \[E'(x)=\lim_{h \to 0}\frac{E(x+h)-E(x)}{h}=E(x)\underbrace{\lim_{h \to 0}\frac{E(h)-1}{h}}_{{\color{red}=1}}=E(x).\]
Properties of the exponential function 4/4
Indeed, \[\frac{E(h)-1}{h}=\frac{1}{h}\sum_{n=1}^{\infty}\frac{h^n}{n!}=\sum_{n=1}^{\infty}\frac{h^{n-1}}{n!},\]
hence \[\begin{aligned} \left|\frac{1}{h}(E(h)-1)-1\right| &\leq \sum_{n=2}^{\infty}\frac{|h|^{n-1}}{n!}=|h|\sum_{n=2}^{\infty}\frac{|h|^{n-2}}{n!}\\ &\leq |h|E(|h|) \underbrace{\leq}_{{\color{red}|h| \leq 1}} |h|e \ _{\overrightarrow{h \to 0}}\ 0. \end{aligned}\]
We have proved that \(E'(x)=E(x)\) for all \(x\in\mathbb R\).
In particular, \(E\) is continuous on \(\mathbb{R}\).
In the next theorem we summarize what we have proved.
Theorem
Theorem. We know that \[\lim_{n \to \infty}\left(1+\frac{x}{n}\right)^n=e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=E(x).\] The exponential function \(\mathbb R\ni x\mapsto e^x\) satisfies the following properties:
\(e^x\) is continuous and differentiable for all \(x \in \mathbb{R}\),
\((e^x)'=e^x\),
\(e^x\) is strictly increasing on \(\mathbb{R}\) and \(e^x>0\) for all \(x \in \mathbb{R}\),
\(e^xe^y=e^{x+y}\) for all \(x, y\in\mathbb R\),
\(\lim_{x \to +\infty}e^x=+\infty\) and \(\lim_{x\to -\infty}e^{x}=0\),
\(\lim_{x \to +\infty}x^{-n}e^{x}=0\) for all \(n \in \mathbb{N}\).
Proof. We have proved (a)-(e). We only prove (f).
Graph of \(f(x)=e^x\)
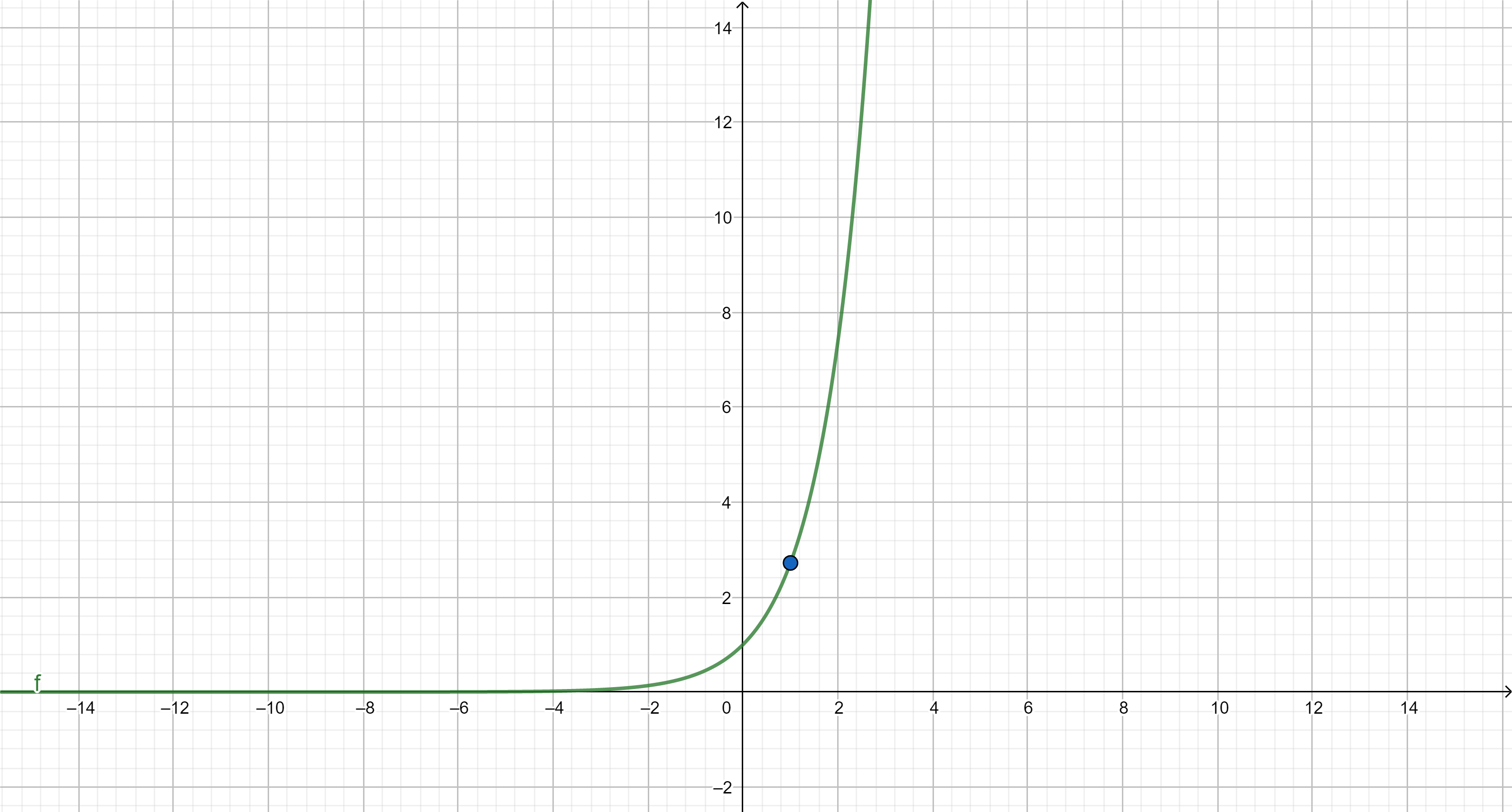
Note that \[e^x=\sum_{k=0}^{\infty}\frac{x^k}{k!}>\frac{x^{n+1}}{(n+1)!},\] so that \[x^ne^{-x}<\frac{(n+1)!}{x}\ _{\overrightarrow{x \to \infty}}\ 0,\] which gives the desired claim.$$\tag*{$\blacksquare$}$$
Remark. Item (f) says that \(e^x\) tends to \(+\infty\) faster that any polynomial.
If \(P(x)=\sum_{k=0}^nc_kx^k\), where \(c_1,\ldots,c_n \in \mathbb{R}\), then \[0 \leq \left|\frac{P(X)}{e^x}\right| \leq \frac{\sum_{k=0}^n|c_k|x^k}{e^x} \ _{\overrightarrow{x \to \infty}}\ 0.\]
The logarithm function
The logarithm function 1/4
Since the exponential function \(E(x)=e^x\) is strictly increasing and differentiable on \(\mathbb{R}\) it has an inverse function \(L\), which is also strictly increasing and differentiable and whose domain is \(E[\mathbb{R}]=(0,\infty)\).
\(L\) is defined by \[E(L(y))=y \quad \text{ for all }\quad y>0\] or, equivalently, \(L(E(x))=x\) for all \(x \in \mathbb{R}\).
Differentiating the latter equation \[1=(x)'=(L(E(x)))'=L'(E(x))E'(x)=L'(E(x))E(x).\] Thus \(L'(E(x))=\frac{1}{E(x)}\), hence
\[L'(y)=\frac{1}{y} \quad \text{ for all }\quad y>0.\]
The logarithm function 2/4
Writing \(u=E(x)\) and \(v=E(y)\) note that \[\begin{aligned} L(uv)=L(E(x)E(y))&=L(E(x+y))\\ &=x+y=L(u)+L(v)\quad \text{ for }\quad u,v>0. \end{aligned}\]
From now on we will write \({\color{red}\log(x)=L(x)}\).
Since \(\lim_{x \to +\infty}e^x=+\infty\) and \(\lim_{x \to -\infty}e^x=0\), we conclude \[\lim_{x \to \infty}\log(x)=+\infty,\quad \text{ and }\quad \lim_{x \to 0}\log(x)=\infty.\]
The logarithm function 3/4. Definition of \(x^{\alpha}\)
Since \(x=E(L(x))\), it is easily seen that \[x^n=E(nL(x)) \quad \text{ and }\quad x^{1 / m}=E\left(\frac{1}{m}L(x)\right) \quad \text{ for }\quad n,m \in \mathbb{N}.\] Thus \[x^{\alpha}=E(\alpha L(x)) \quad \text{ if }\quad \alpha \in \mathbb{Q}.\]
It also makes sense to define \[x^{\alpha}=E(\alpha L(x)) \quad \text{ for }\quad \alpha \in \mathbb{R} \quad \text{ and }\quad x>0.\]
The continuity and monotonicity of \(E\) and \(L\) show that everything makes sense and this definition coincides with
\[x^{\alpha}=\sup\{x^p\;:\;p<\alpha, \ p \in \mathbb{Q}\} \quad \text{ if }\quad \alpha \in \mathbb{R}\quad \text{ and }\quad x>1.\]
The logarithm function 4/4
If we differentiate \[x^{\alpha}=E(\alpha aL(x)),\] then \[(x^{\alpha})'=E'(\alpha L(x))\frac{\alpha}{x}={\color{blue}\alpha x^{\alpha-1}}.\]
Finally note that \[\lim_{x \to \infty}x^{-\alpha}\log(x)=0\quad \text{ for every }\quad \alpha>0.\] That is, \(\log(x)\) tends to \(+\infty\) slower that any power of \(x\).
Indeed, since \(x^{\alpha} \ _{\overrightarrow{x \to \infty}}\ +\infty\), by L’Hôpital’s rule \[\lim_{x \to \infty}\frac{\log(x)}{x^{\alpha}}\underbrace{=}_{{\color{red}L'H{{o}}pital}}\lim_{x \to \infty}\frac{\frac{1}{x}}{\alpha x^{\alpha-1}}=\lim_{x \to \infty}\frac{1}{\alpha x^{\alpha}}=0.\]
Power series
Power series
Power series. Given a sequence \((c_n)_{n \in \mathbb{N}_0}\), where \(c_n \in \mathbb{R}\), the series \[{\color{blue}\sum_{n=0}^{\infty}c_nx^n, \ \ x \in \mathbb{R}}\] is called a power series.
The numbers \(c_n\) are called the coefficients of the series.
Example 1. \(\sum_{n=0}^{\infty}x^n\).
Example 2. \(e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}\).
Radius of convergence
Radius of convergence. Given the power series \[\sum_{n=0}^{\infty}c_nx^n\] set \[{\color{red}\alpha=\limsup_{n \to \infty}\sqrt[n]{|c_n|}, \quad \text{ and } \quad R=\frac{1}{\alpha}}.\] If \(\alpha=0\), then \(R=+\infty\).
The number \(R\) is called the radius of convergence of \(\sum_{n=0}^{\infty}c_nx^n\).
Theorem
Theorem. The series \(\sum_{n=0}^{\infty}c_nx^n\)
converges if \(|x|<R\), and
diverges if \(|x|>R\).
Proof. Consider \(a_n=c_nx^n\) and apply the root test \[\limsup_{n \to \infty}\sqrt[n]{|a_n|}=|x|\limsup_{n \to \infty}\sqrt[n]{|c_n|}=\frac{|x|}{R}.\qquad \tag*{$\blacksquare$}\]
Example 1. \(\sum_{n=0}^{\infty}n^nx^n\) has \(R=0\)
Example 2. \(\sum_{n=0}^{\infty}\frac{x^n}{n!}\) has \(R=+\infty\).
Examples
Example 2. Hence if \(\sum_{n=0}^{\infty}\frac{x^n}{n!}\), then \(R=+\infty\) since \[\alpha=\limsup_{n \to \infty}\sqrt[n]{\frac{1}{n!}}=0.\]
Example 3. \(\sum_{n=0}^{\infty}x^n\) has \(R=1\). If \(|x|=1\) the series \(\sum_{n=0}^{\infty}x^n\) diverges. We also know \[\sum_{n=0}^{\infty}x^n=\frac{1}{1-x}\quad \text{ if }\quad |x|<1.\]
Example 4. \(\sum_{n=1}^{\infty}\frac{x^n}{n}\) has \(R=1\). If \(x=1\) the series diverges since \[\sum_{n=1}^{\infty}\frac{1}{n}=+\infty.\] If \(x=-1\) then the series converges since \[\left|\sum_{n=1}^{\infty}\frac{(-1)^n}{n}\right|<\infty.\]
Taylor’s theorem
Taylor’s theorem
Taylor’s theorem. Suppose \(f:[a,b] \to \mathbb{R}\), \(n \in \mathbb{N}\), \(f^{(n-1)}\) is continuous on \([a,b]\), and \(f^{(n)}(t)\) exists for every \(t \in (a,b)\). Let \(\alpha,\beta \in [a,b]\) be distinct and define \[{\color{red}P(t)=\sum_{k=0}^{n-1}\frac{f^{(k)}(\alpha)}{k!}(t-\alpha)^k}.\]
then there exists a point \(x \in (\alpha,\beta)\) such that \[\qquad \qquad \qquad f(\beta)=P(\beta)+\frac{f^{(n)(x)}}{n!}(\beta-\alpha)^n\qquad \qquad \qquad {\color{purple}(*)}\]
Remark. For \(n=1\) this is just the mean–value theorem. In general, the theorem says that \(f\) can be approximated by a polynomial of degree \(n-1\) and that (*) allows us to estimate the error term if we know bounds on \(|f^{(n)}(x)|\).
Proof. Let \(M\) be a number such that \[f(\beta)=P(\beta)+M(\beta-\alpha)^n.\] For \(a \leq t \leq b\) set
\[g(t)=f(t)-P(t)-M(t-\alpha)^n.\]
We have to show \({\color{blue}n!M=f^{(n)}(x)}\) for some \(x \in (\alpha,\beta)\).
Since \[P(t)=\sum_{k=0}^{n-1}\frac{f^{(k)}(\alpha)}{k!}(t-\alpha)^k\] we have that \(P^{(n)}(t)=0\). Thus \[g^{(n)}(t)=f^{(n)}(t)-n!M \quad \text{ for }\quad t \in (\alpha,\beta)\] (since \((x^n)^{(n)}=n!\)).
The proof will be completed if we show that \({\color{red}g^{(n)}(x)=0}\) for some \(x \in (\alpha,\beta)\). Since \(P^{(k)}(\alpha)=f^{(k)}(\alpha)\) for \(k=0,1,2,\ldots,n-1\), hence we have \[{\color{brown}g(\alpha)=g'(\alpha)=\ldots=g^{(n-1)}(\alpha)=0}.\] Our choice of \(M\) shows that \({\color{brown}g(\beta)=0}\).
Hence by the mean-value theorem \[g'(x_1)=0\quad \text{ for some }\quad x_1 \in (\alpha,\beta)\] since \(0=g(\alpha)-g(\beta)=(\beta-\alpha)g'(x_1)\).
Using that \(g'(\alpha)=0\) we continue and obtain \[0=g'(x_1)-g'(\alpha)=(x_1-\alpha)g''(x_2) \quad \text{ for some }\quad \alpha<x_2<x_1.\] Thus \(g''(x_2)=0\).
Repeating the previous arguments, after \(n\) steps we obtain \[{\color{red}g^{(n)}(x_n)=0}\quad \text{ for some }\quad \alpha<x_n<x_{n-1}<\ldots<x_1<\beta.\] This completes the proof. $$\tag*{$\blacksquare$}$$
Theorem
Theorem (Taylor’s expansion formula). Suppose that \(f:[a,b] \to \mathbb{R}\) is \(n\)-times continuously differentiable on \([a,b]\) and \(f^{(n+1)}\) exists in the open interval \((a,b)\). For any \(x,x_0 \in [a,b]\) and \(p>0\) there exists \(\theta \in (0,1)\) such that \[{\color{blue}f(x)=\sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k+r_n(x),}\] where \(r_n(x)\) is the Schlömlich–Roche remainder function defined by \[{\color{teal}r_n(x)=\frac{f^{(n+1)}(x_0+\theta(x-x_0))}{n!p}(1-\theta)^{n+1-p}(x-x_0)^{n+1}}.\]
For \(x,x_0 \in [a,b]\) set \[r_n(x)=f(x)-\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k.\]
Wlog we may assume that \(x>x_0\). For \(z\in [x_0,x]\) define \[\phi(z)=f(x)-\sum_{k=0}^n\frac{f^{(k)}(z)}{k!}(x-z)^k.\]
We have \(\phi(x_0)=r_n(x)\) and \(\phi(x)=0\), and \(\phi'\) exists in \((x_0,x)\) and
\[\phi'(z)=-\frac{f^{(n+1)}(z)}{n!}(x-z)^{n}.\]
Indeed, by the telescoping we obtain \[\begin{aligned} \phi'(z)&=-\left(\sum_{k=0}^{n}\frac{f^{(k)}(z)}{k!}(x-z)^k\right)' \\&=-\sum_{k=0}^n \left({\color{red}\frac{f^{(k+1)}(z)}{k!}(x-z)^k}-{\color{blue}\frac{f^{(k)}(z)}{k!}k(x-z)^{k-1}}\right) \\&={\color{red}\sum_{k=1}^n\frac{f^{(k)}(z)}{(k-1)!}(x-z)^{k-1}}-{\color{blue}\sum_{k=0}^n\frac{f^{(k+1)}(z)}{k!}(x-z)^{k}} \\&=-\frac{f^{(n+1)}(z)}{n!}(x-z)^{n}. \end{aligned}\]
Let \(\psi(z)=(x-z)^p\), then \(\psi\) is continuous on \([x_0,x]\) with non-vanishing derivative on \((x_0,x)\).
By the mean-value theorem \[\frac{\phi(x)-\phi(x_0)}{\psi(x)-\psi(x_0) }=\frac{\phi'(c)}{\psi'(c)} \quad \text{ for some }\quad c \in (x_0,x ).\]
Thus, setting \({\color{brown}c=x_0+\theta(x-x_0)}\), \[\begin{aligned} r_n(x)&=\underbrace{\phi(x_0)}_{{\color{red}=r_n(x)}}-\underbrace{\phi(x)}_{{\color{red}=0}}=-(\psi(x)-\psi(x_0))\frac{\phi'(c)}{\psi'(c)} \\&=\frac{f^{(n+1)}(c)}{n!}(x-c)^n\frac{-(x-x_0)^p}{-p(x-c)^{p-1}}= \\&={\color{brown}\frac{f^{(n+1)}(x_0+\theta(x-x_0))}{pn!}(1-\theta)^{n+1-p}(x-x_0)^{n+1}}.\end{aligned}\qquad\blacksquare\]
Corollary
Under the assumptions of the previous theorem.
Lagrange remainder. If \(p=n+1\) we obtain the Taylor formula with the Lagrange remainder: \[{\color{red}r_n(x)=\frac{f^{(n+1)}(x_0+\theta(x-x_0))}{(n+1)!}(x-x_0)^{n+1}}.\]
Cauchy remainder. If \(p=1\) we obtain the Taylor formula with the Cauchy remainder: \[{\color{blue}r_n(x)=\frac{f^{(n+1)}(x_0+\theta(x-x_0))}{n!}(1-\theta)^n(x-x_0)^{n+1}}.\]