25. Riemann Integrals PDF
Partitions
Partition. Let \([a, b]\) be a given interval. By a partition \(P\) of \([a, b]\) we mean a finite set of points \[a=x_0 \leq x_1 \leq \ldots \leq x_{n-1} \leq x_n=b.\]
Example 1. If \([a,b]=[0,1]\), then \(\{0,\frac{1}{2},1\}\) is a partition.
Example 2. If \([a,b]=[0,1]\), then \[\left\{\frac{k}{n}\;:\;k=0,1,\ldots,n \right\}\] is a partition for every \(n \in \mathbb{N}\).
Upper and lower Riemann sums
Suppose \(f:[a,b]\to \mathbb R\) is a bounded function. Corresponding to each partition \(P\) of \([a, b]\) we put \[\begin{gathered} m_i=\inf_{x \in [x_{i-1},x_i]}f(x), \quad \text{ and } \quad M_i=\sup_{x \in [x_{i-1},x_i]}f(x),\\ \Delta x_i=x_{i}-x_{i-1}. \end{gathered}\]
Upper and lower Riemann sums. We define \[U(P,f)=\sum_{i=1}^{n}M_i\Delta x_i,\] \[L(P,f)=\sum_{i=1}^{n}m_i\Delta x_i.\]
We always have that \(L(P,f)\le U(P,f)\).
Examples
Example 1. If \(f(x)=x\) and \(P=\{0,\frac{1}{2},1\}\), then \[\begin{aligned} U(P,f)=\frac{1}{2}\cdot \frac{1}{2}+1 \cdot \frac{1}{2}=\frac{3}{4}, \quad \text{ and } \quad L(f,L)=0 \cdot \frac{1}{2}+\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4}. \end{aligned}\]
Example 2. If \(f(x)=x^2\) and \[P=\left\{\frac{k}{n}\;:\; k=0,1,\ldots,n\right\},\] then \[U(P,f)=\sum_{i=1}^{n}\frac{1}{n}\left(\frac{{\color{red}i}}{n}\right)^2, \quad \text{ and } \quad L(P,f)=\sum_{i=1}^{n}\frac{1}{n}\left(\frac{{\color{blue}i-1}}{n}\right)^2.\]
Riemann sums - geometric interpretation
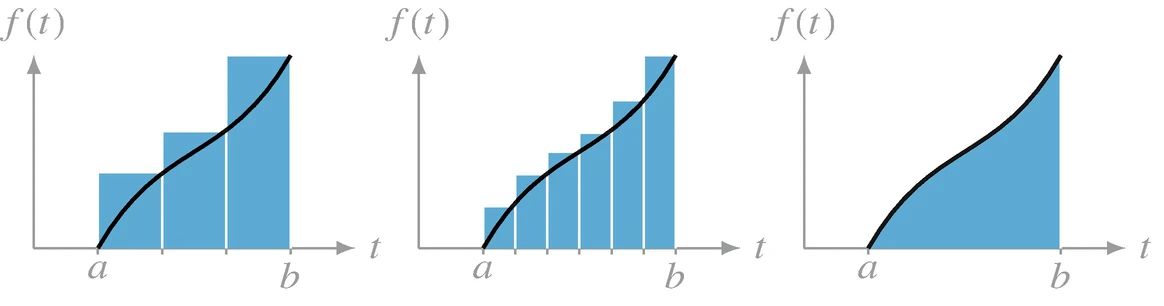
Upper and lower Riemann integral
Upper and lower Riemann integral. We define the upper and lower Riemann integrals of \(f\) over \([a, b]\) to be \[\begin{aligned} \underline{\int_a^b}f(x)\,dx=\sup_P L(P,f), \quad \text{ and } \quad \overline{\int_a^b}f(x)\,dx=\inf_P U(P,f), \end{aligned}\] where the inf and the sup are taken over all partitions \(P\) of \([a,b]\).
Riemann integral of \(f\) over \([a, b]\). If the upper and lower integrals are equal, we say that \(f:[a, b]\to \mathbb R\) is Riemann integrable on \([a, b]\), we write \(f \in \mathcal{R}([a, b])\) and we denote the common value (which is called Riemann integral of \(f\) over \([a, b]\)) by \[\int_a^b f(x)\,dx= \underline{\int_a^b}f(x)\,dx= \overline{\int_a^b}f(x)\,dx.\]
Riemann integral is well-defined
Fact. The upper and lower integrals are defined for every bounded function.
Proof. Let \[\begin{aligned} m &=\inf_{x \in [a,b]} f(x),\\ M& =\sup_{x \in [a,b]}f(x). \end{aligned}\] Then \[m \leq f(x) \leq M \quad \text{ for all }\quad x \in [a,b].\] Therefore \[m(b-a) \leq L(P,f) \leq U(P,f) \leq M(b-a)\] for every partition \(P\).$$\tag*{$\blacksquare$}$$
Question of the integrability of \(f\)
Example. There is a bounded function \(f\) which is not integrable.
Proof. Let us define \(f\) on \([0,1]\) to be \[f(x)=\begin{cases} 1 \text{ if }x \in \mathbb{Q},\\ 0 \text{ if }x\not\in \mathbb{Q}. \end{cases}\] Let us recall
Fact (*). In any interval \([c,d]\) such that \(c<d\) there is a rational and irrational number.
By the fact \({\color{purple}(*)}\), for every partition \(P\) of \([0, 1]\), we have
\[U(P,f)=\sum_{i=1}^{n}M_i\Delta x_i=\sum_{i=1}^n1\cdot \Delta x_i =1,\] \[L(P,f)=\sum_{i=1}^{n}m_i\Delta x_i=\sum_{i=1}^n 0\cdot \Delta x_i=0.\]
Therefore
\[\underline{\int_a^b}f(x)\,dx=\sup_P L(P,f)=0, \quad \text{ and } \quad \overline{\int_a^b}f(x)\,dx=\inf_P U(P,f)=1.\]
Hence \({\color{red}\underline{\int_a^b}f(x)\,dx \neq \overline{\int_a^b}f(x)\,dx}\) and \(f\) is not integrable.$$\tag*{$\blacksquare$}$$
Refinements
Refinement. We say that the partition \(P^{*}\) is a refinement of \(P\) if \(P^{*} \supseteq P\).
Common refinement. Given two partitions, \({\color{red}P_1}\) and \({\color{blue}P_2}\),we say that \(P^{*}\) is their common refinement if \[P^{*}={\color{red}P_1} \cup {\color{blue}P_2}.\]
Example. If \([a,b]=[0,2]\) and \(P_1=\{0,\frac{1}{2},1,2\}\), \(P_2=\{0,\frac{1}{4},\frac{1}{2},\frac{3}{2},2\}\) are partitions, then their common refinement is \[P^{*}=\left\{0,\frac{1}{4},\frac{1}{2},1,\frac{3}{2},2\right\}.\]
Theorem
Theorem. If \(P^*\) is a refinement of \(P\), then \[\begin{aligned} \color{red}L(P,f) &\color{red}\leq L(P^{*},f),\\ \color{blue}U(P^{*},f) &\color{blue}\leq U(P,f). \end{aligned}\]
Proof. We prove the first statement.
Suppose first that \(P^{*}\) contains just one point more than \(P\). Let this extra point be \(x^{*}\), and suppose \[x_{i-1} \leq x^{*} \leq x_i \quad \text{ for some }\quad i \in \{1,2,\ldots,n\}.\]
Let \[\begin{gathered} m_i=\inf_{x \in [x_{i-1},x_i]}f(x),\\ w_1=\inf_{x \in {\color{red}[x_{i-1},x^{*}]}}f(x), \quad \text{ and } \quad w_2=\inf_{x \in {\color{blue}[x^{*},x_i]}}f(x) \end{gathered}\]
Then \(w_1\ge m_i\) and \(w_2\ge m_i\) and consequently \[\begin{gathered} L(P^{*},f)-L(P,f)={\color{red}w_1(x^{*}-x_{i-1})}+{\color{blue}w_2(x_i-x^*)} -{\color{purple}m_i(x_i-x_{i-1})}\\ ={(w_1-m_i)(x^{*}-x_{i-1})}+{(w_2-m_i)(x_i-x^*)} \geq 0. \end{gathered}\]
Finally, if \(P^*\) contains \({\color{brown}k}\) points more than \(P\), we repeat this reasoning \({\color{brown}k}\) times. The proof of the second statement is analogous.$$\tag*{$\blacksquare$}$$
Claim (*). For two partitions \(P_1, P_2\) of an interval \([a, b]\) one has \[L(P_1,f) \leq U(P_2,f).\]
Proof. Let \(P^{*}=P_1\cup P_2\) be the common refinement of two partitions \(P_1\) and \(P_2\). By the previous theorem \[{\color{red}L(P_1,f) \leq L(P^*,f)} \leq {\color{blue}U(P^*,f) \leq U(P_2,f)}.\]
Theorem. For any bounded function \(f:[a,b]\to \mathbb R\) we have \[\underline{\int_a^b}f(x)dx \leq \overline{\int_a^b}f(x)dx.\]
Proof. By the Claim (*) for two partitions \(P_1, P_2\) of an interval \([a, b]\) one has \[L(P_1,f) \leq U(P_2,f).\] Then \[\underline{\int_a^b}f(x)\,dx=\sup_{P_1} L(P_1,f)\le \inf_{P_2} U(P_2,f)= \overline{\int_a^b}f(x)\,dx,\] This completes the proof of the theorem.$$\tag*{$\blacksquare$}$$
Theorem. A function \(f \in \mathcal{R}([a, b])\) if and only if the following condition (\(\mathcal R\)) holds:
For every \(\varepsilon>0\) there is a partition \(P\) of \([a, b]\) such that \[\begin{aligned} \qquad\qquad \qquad U(P,f)-L(P,f)<\varepsilon. \qquad\qquad \qquad {\color{purple} (\mathcal R)} \end{aligned}\]
Proof. By the previous theorem, for every partition \(P\) we have \[L(P,f) \leq \underline{\int_a^b}f(x)dx\leq \overline{\int_a^b}f(x)dx \leq U(P,f).\] Thus the condition (\(\mathcal R\)) implies \[0\le \overline{\int_a^b}f(x)dx-\underline{\int_a^b}f(x)dx\le U(P,f)-L(P,f)<\varepsilon.\] Since \(\varepsilon>0\) is arbitrary \(\overline{\int_a^b}f(x)dx=\underline{\int_a^b}f(x)dx\), hence \(f \in \mathcal{R}(\alpha)\).
Conversely, suppose that \(f \in \mathcal{R}(\alpha)\). Then for every \(\varepsilon>0\) there are partitions \({\color{red}P_1}\) and \({\color{blue}P_2}\) such that \[\begin{aligned} {\color{red}\underline{\int_a^b}f(x)dx-L(P_1,f)<\frac{\varepsilon}{2}} \quad \text{ and } \quad {\color{blue}U(P_2,f)-\overline{\int_a^b}f(x)dx<\frac{\varepsilon}{2}}. \end{aligned}\]
We choose \(P\) to be the common refinement of \({\color{red}P_1}\) and \({\color{blue}P_2}\). Then \[\begin{gathered} U(P,f) \leq U(P_2,f)\\ \leq \overline{\int_a^b}f(x)dx+\frac{\varepsilon}{2}= {\int_a^b}f(x)dx+\frac{\varepsilon}{2}= \underline{\int_a^b}f(x)dx+\frac{\varepsilon}{2}\\ \leq L(P_1,f)+\varepsilon \leq L(P,f)+\varepsilon. \end{gathered}\] This proves condition (\(\mathcal R\)) and completes the proof of the theorem. $$\tag*{$\blacksquare$}$$
Theorem (**). If condition (\(\mathcal R\)) holds for \(P=\{x_0,\ldots,x_n\}\) and if \(s_i,t_i\) are arbitrary points in \([x_{i-1},x_i]\), then \[\sum_{i=1}^{n}|f(s_i)-f(t_i)|\Delta x_i<\varepsilon.\]
Proof. Note that \(f(s_i),f(t_i)\) lies in \([m_i,M_i]\), hence by the triangle inequality \[|f(t_i)-f(s_i)| \leq \underbrace{M_i-m_i}_{\text{length}}.\] Hence \[\begin{aligned} &\sum_{i=1}^{n}|f(s_i)-f(t_i)|\Delta x_i \leq \sum_{i=1}^{n}(M_i-m_i)\Delta x_i =\overline{\int_a^b}f(x)dx -\underline{\int_a^b}f(x)dx <\varepsilon. \end{aligned}\] This completes the proof. $$\tag*{$\blacksquare$}$$
Theorem. If \(f \in \mathcal{R}([a, b])\) and the hypotheses of \({\color{brown}(**)}\) hold, then \[\left|\sum_{i=1}^nf(t_i)\Delta x_i-\int_a^bf(x)\,dx\right|<\varepsilon.\]
Proof. It is enough to note that \[\begin{aligned} L(P,f) &\leq \sum_{i=1}^nf(t_i)\Delta x_i \leq U(P,f),\\ L(P,f) &\leq \int_a^b f(x)\;dx \leq U(P,f).\quad\end{aligned}\qquad\blacksquare\]
Riemann integrability for continuous functions
Theorem. If \(f\) is continuous on \([a, b]\) then \(f \in \mathcal{R}([a,b])\).
Proof. Let \(\varepsilon>0\) be given. Choose \(\eta>0\) such that \(\eta(b-a)<\varepsilon.\) Recall that if \(f\) is continuous on \([a,b]\), then it is also uniformly continuous.
Hence, there is \(\delta>0\) such that \(|f(x)-f(t)|<\eta\) if \(|t-x|<\delta.\)
In particular, that means that \({\color{red}M_i-m_i<\eta}\) for every partition such that \(\Delta x_i<\delta\).
Hence, \[\begin{aligned} U(P,f)-L(P,f)=\sum_{i=1}^n(M_i-m_i)\Delta x_i \leq \eta \sum_{i=1}^n \Delta x_i=\eta(b-a)<\varepsilon. \end{aligned}\]
The proof is completed. $$\tag*{$\blacksquare$}$$
Riemann integrability for monotonic functions
Theorem. If \(f:[a, b]\to \mathbb R\) is monotonic, then \(f \in \mathcal{R}([a, b])\).
Proof. Let \(\varepsilon>0\) be given. For \(n \in \mathbb{N}\) choose a partition \(P\) such that \({\color{red}\Delta x_i=\frac{b-a}{n}}\). We suppose that \(f\) is monotonically increasing. Then \[{\color{blue}M_i-m_i=f(x_i)-f(x_{i-1}).}\] Hence, if \(n\) is taken large enough, we obtain \[\begin{aligned} U(P,f)-L(P,f)&=\sum_{i=1}^n(M_i-m_i)\Delta x_i \\ & ={\color{red}\frac{b-a}{n}}\sum_{i=1}^n{\color{blue}f(x_i)-f(x_{i-1})}=\frac{b-a}{n}(f(b)-f(a))<\varepsilon, \end{aligned}\] and we are done, the proof is analogous in the other case.$$\tag*{$\blacksquare$}$$
Example
Example 1. Let \[f(x)=\begin{cases} x &\text{ for }x \in [0,1],\\ x^2+5 &\text{ for }x\in (1,2], \\ x^3+9 &\text{ for }x\in(3,4]. \end{cases}\] Prove that \(f\) is Riemann integrable on \([0,4]\).
Solution. \(f\) is increasing, so \(f\) is Riemann integrable by the previous theorem.